14_RA

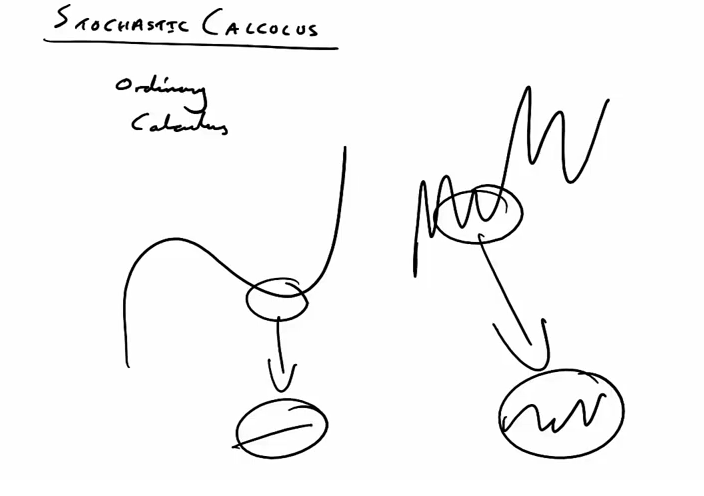
The Euler–Maruyama method (also called the Euler method) is a method for the approximate numerical solution of a stochastic differential equation (SDE) [1]. It is a simple generalization of the Euler method for ordinary differential equations to stochastic differential equations. It is named after Leonhard Euler and Gisiro Maruyama. Unfortunately, the same generalization cannot be done for any arbitrary deterministic method.

The Milstein method is a technique for the approximate numerical solution of a stochastic differential equation [2]. It is named after Grigori N. Milstein who first published the method in 1974.

The Runge–Kutta method is a technique for the approximate numerical solution of a stochastic differential equation. It is a generalisation of the Runge–Kutta method for ordinary differential equations to stochastic differential equations (SDEs) [3]. Importantly, the method does not involve knowing derivatives of the coefficient functions in the SDEs.

---

References

1. https://en.wikipedia.org/wiki/Euler%E2%80%93Maruyama_method

2. https://en.wikipedia.org/wiki/Milstein_method

3. https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_method_(SDE)