23_R

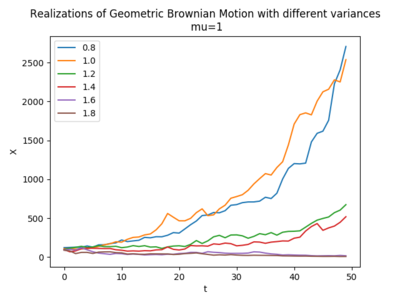
Geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion (also called a Wiener process) with drift [1]. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical finance to model stock prices in the Black–Scholes model.

A stochastic process St is said to follow a GBM if it satisfies the following stochastic differential equation (SDE):

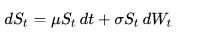
where Wt is a Wiener process or Brownian motion, and μ ('the percentage drift') and σ ('the percentage volatility') are constants. The former is used to model deterministic trends, while the latter term is often used to model a set of unpredictable events occurring during this motion.

Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction [2]. It is named after Leonard Ornstein and George Eugene Uhlenbeck.

The Ornstein–Uhlenbeck process is a stationary Gauss–Markov process, which means that it is a Gaussian process, a Markov process, and is temporally homogeneous. In fact, it is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables.[1] Over time, the process tends to drift towards its mean function: such a process is called mean-reverting.

The process can be considered to be a modification of the random walk in continuous time, or Wiener process, in which the properties of the process have been changed so that there is a tendency of the walk to move back towards a central location, with a greater attraction when the process is further away from the center. The Ornstein–Uhlenbeck process can also be considered as the continuous-time analogue of the discrete-time AR(1) process.

The Ornstein–Uhlenbeck process is defined by the following stochastic differential equation:

where θ > 0 and σ > 0 are parameters and Wt denotes the Wiener process.

An additional drift term is sometimes added:

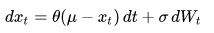
where μ is a constant. In financial mathematics, this is also known as the Vasicek model [3].

Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of one-factor short rate model as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives, and has also been adapted for credit markets. It was introduced in 1977 by Oldřich Vašíček, and can be also seen as a stochastic investment model.

Mean reversion is a financial term for the assumption that a stock's price will tend to move to the average price over time.

Using mean reversion in stock price analysis involves both identifying the trading range for a stock and computing the average price using analytical techniques taking into account considerations such as earnings, etc.

When the current market price is less than the average price, the stock is considered attractive for purchase, with the expectation that the price will rise. When the current market price is above the average price, the market price is expected to fall. In other words, deviations from the average price are expected to revert to the average. This knowledge serves as the cornerstone of multiple trading strategies.

In finance, the term "mean reversion" has a different meaning from "return or regression to the mean" in statistics [5]. In statistics, regression toward the mean (or regression to the mean) is the phenomenon that arises if a sample point of a random variable is extreme (nearly an outlier), a future point will be closer to the mean or average on further measurements. To avoid making incorrect inferences, regression toward the mean must be considered when designing scientific experiments and interpreting data. Historically, what is now called regression toward the mean was also called reversion to the mean and reversion to mediocrity.

---

References

1. https://en.wikipedia.org/wiki/Geometric_Brownian_motion

2. https://en.wikipedia.org/wiki/Ornstein%E2%80%93Uhlenbeck_process

3. https://en.wikipedia.org/wiki/Vasicek_model

4. https://en.wikipedia.org/wiki/Mean_reversion_(finance)

5. https://en.wikipedia.org/wiki/Regression_toward_the_mean