24_R
- hrafnulf13
- Dec 16, 2020
- 3 min read
Stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process [1]. SDEs are used to model various phenomena such as unstable stock prices or physical systems subject to thermal fluctuations. Typically, SDEs contain a variable which represents random white noise calculated as the derivative of Brownian motion or the Wiener process. However, other types of random behaviour are possible, such as jump processes.
Stochastic differential equations originated in the theory of Brownian motion, in the work of Albert Einstein and Smoluchowski. These early examples were linear stochastic differential equations, also called 'Langevin' equations after French physicist Langevin, describing the motion of a harmonic oscillator subject to a random force. The mathematical theory of stochastic differential equations was developed in the 1940s through the groundbreaking work of Japanese mathematician Kiyosi Itô, who introduced the concept of stochastic integral and initiated the study of nonlinear stochastic differential equations. Another approach was later proposed by Russian physicist Stratonovich, leading to a calculus similar to ordinary calculus.
Brownian motion or the Wiener process was discovered to be exceptionally complex mathematically. The Wiener process is almost surely nowhere differentiable; thus, it requires its own rules of calculus. There are two dominating versions of stochastic calculus, the Itô stochastic calculus and the Stratonovich stochastic calculus. Each of the two has advantages and disadvantages, and newcomers are often confused whether the one is more appropriate than the other in a given situation. Guidelines exist (e.g. Øksendal, 2003) and conveniently, one can readily convert an Itô SDE to an equivalent Stratonovich SDE and back again. Still, one must be careful which calculus to use when the SDE is initially written down.
Ordinary differential equation (ODE) is a differential equation containing one or more functions of one independent variable and the derivatives of those functions [2]. The term ordinary is used in contrast with the term partial differential equation which may be with respect to more than one independent variable.
Stochastic differential equations involve a “noisy” process [3]. This means there is a random component to how the state of a system evolves over time. Ordinary differential equations, on the other hand, are deterministic; no random evolution is present. Both types of differential equations involve evolution of a single tracer over time; picture the center of mass moving under Newton's second law. Ordinary differential equations would be used when the force profile is well-understood and can be determined by the current state, like planetary motion. Stochastic differential equations would be used when the force profile is too complex to be modeled closed-form, like Brownian motion.
Itô calculus, named after Kiyoshi Itô, extends the methods of calculus to stochastic processes such as Brownian motion [4]. It has important applications in mathematical finance and stochastic differential equations. The central concept is the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis.
We use standard calculus when we can analyze a normal function, thus we can differentiate it. So for example, by zooming in to curve, we can find that segments of the curve are straight lines. Yet, when we try to analyze the stochastic processes, those segments will still look like mini-versions of stochastic processes. Therefore you cannot use standard calculus in this case.
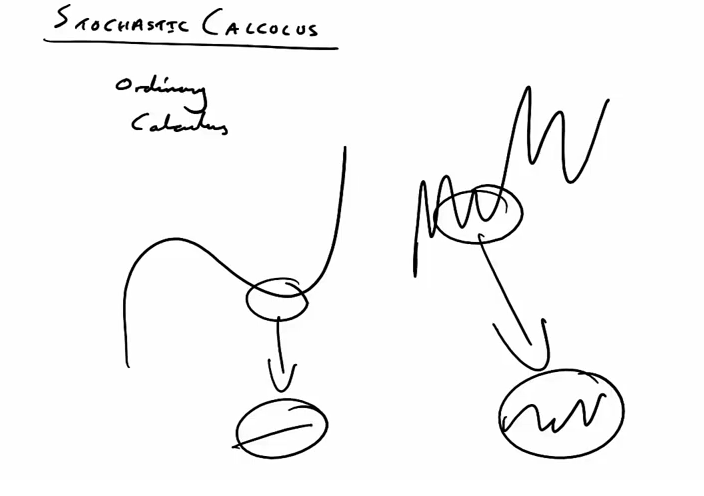
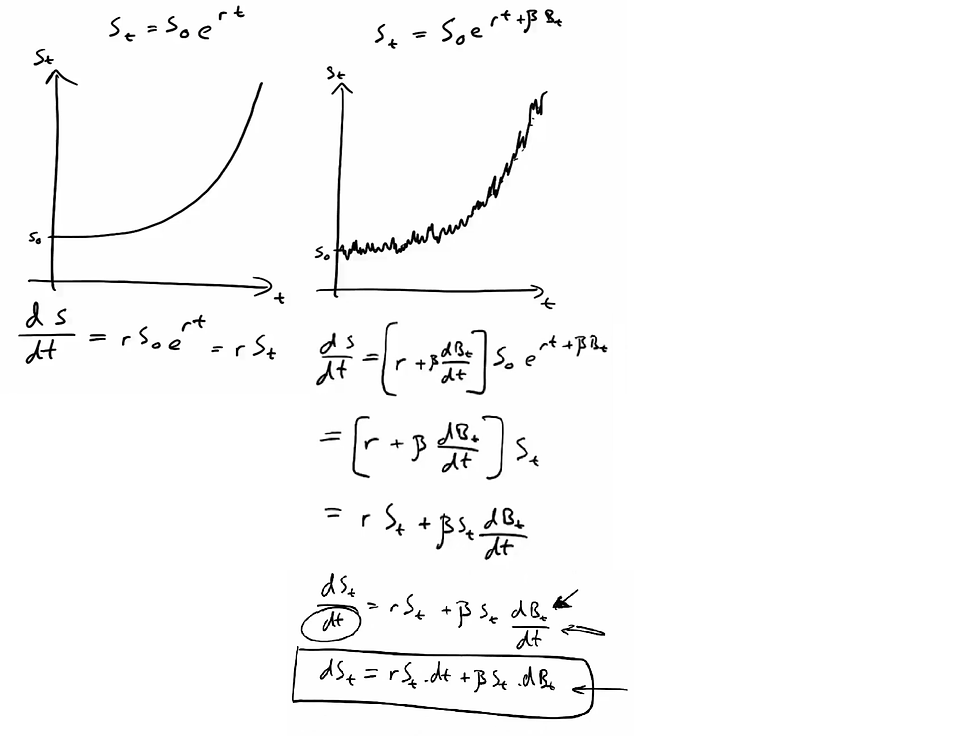
Using example from [5], where comparison of an exponential function and an exponential function containing a brownian motion, leads to a problem of derivation of second function (right one). It is impossible to derive it using simple calculus. Yet, it still possible to calculate the area below the curve, allowing to solve SDE. This is where the Ito integral is used. Ito’s lemma is used for Ito integration.
References
https://en.wikipedia.org/wiki/Stochastic_differential_equation
https://en.wikipedia.org/wiki/Ordinary_differential_equation
https://www.youtube.com/watch?v=rvYfNz2H3Uk
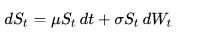

Comments