13_RA
- hrafnulf13
- Dec 9, 2020
- 1 min read
In the 20_R we have described what a Brownian Motion is. In the 20_A we see an example of implementing it.

The Wiener process is characterized by [1]:
W(0) = 0. 20_A clearly satisfy this property.
W(t) is almost surely continuous. All graphs in 20_A are continuous (no discontinuity).
W(t) has independent increments. All the steps of each random walk/path are independent, since they are generated using uniform random variable. Thus it implies the independence of the increments.
W(t) – W(s) ~ N(0, t - s) (for 0 <= s <=t). Brownian motion at any time has an expected value of 0, we can see the distribution is centered around 0. Then histograms as t increases the bell shape is attenuated, thus loses it's shape.

References
https://en.wikipedia.org/wiki/Brownian_motion#Mathematics
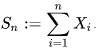

Comments