22_R
- hrafnulf13
- Dec 9, 2020
- 1 min read
In probability theory, Donsker's theorem (also known as Donsker's invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem [1, 2].
Let X1, X2, X3, ... be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1. Let
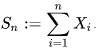
The stochastic process
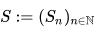
is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by
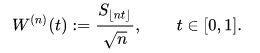
The central limit theorem asserts that

converges in distribution to a standard Gaussian random variable
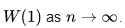
Donsker's invariance principle extends this convergence to the whole function
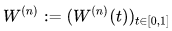
More precisely, in its modern form, Donsker's invariance principle states that: As random variables taking values in the Skorokhod space D[0, 1], the random function
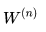
converges in distribution to a standard Brownian motion
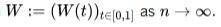
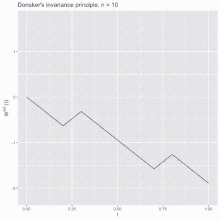
References
https://encyclopediaofmath.org/wiki/Donsker_invariance_principle
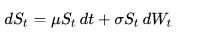

Comments