21_R
- hrafnulf13
- Dec 9, 2020
- 3 min read
Brownian motion is the random motion of particles suspended in a medium (a liquid or a gas) [1].

This is a simulation of the Brownian motion of 5 particles (yellow) that collide with a large set of 800 particles. The yellow particles leave 5 blue trails of random motion and one of them has a red velocity vector.Brownian motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the Equipartition theorem).
This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking through a microscope at pollen of the plant Clarkia pulchella immersed in water. In 1905, almost eighty years later, theoretical physicist Albert Einstein published a paper where he modeled the motion of the pollen particles as being moved by individual water molecules, making one of his first major scientific contributions. This explanation of Brownian motion served as convincing evidence that atoms and molecules exist and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 "for his work on the discontinuous structure of matter". The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.
The many-body interactions that yield the Brownian pattern cannot be solved by a model accounting for every involved molecule. In consequence, only probabilistic models applied to molecular populations can be employed to describe it. Two such models of the statistical mechanics, due to Einstein and Smoluchowski are presented below. Another, pure probabilistic class of models is the class of the stochastic process models. There exist sequences of both simpler and more complicated stochastic processes which converge (in the limit) to Brownian motion (see random walk and Donsker's theorem).
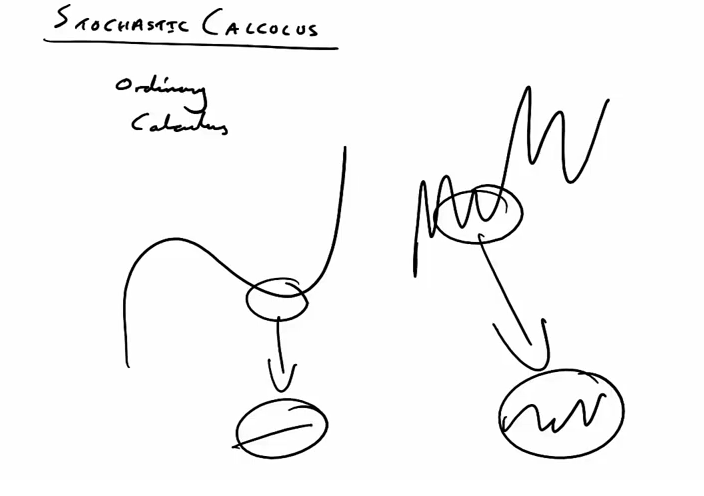
In mathematics, Brownian motion is described by the Wiener process, a continuous-time stochastic process named in honor of Norbert Wiener [2, 3]. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary independent increments) and occurs frequently in pure and applied mathematics, economics and physics.
The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the Wiener process is used to represent the integral of a white noise Gaussian process, and so is useful as a model of noise in electronics engineering (see Brownian noise), instrument errors in filtering theory and disturbances in control theory.
The Wiener process has applications throughout the mathematical sciences. In physics it is used to study Brownian motion, the diffusion of minute particles suspended in fluid, and other types of diffusion via the Fokker–Planck and Langevin equations. It also forms the basis for the rigorous path integral formulation of quantum mechanics (by the Feynman–Kac formula, a solution to the Schrödinger equation can be represented in terms of the Wiener process) and the study of eternal inflation in physical cosmology. It is also prominent in the mathematical theory of finance, in particular the Black–Scholes option pricing model.
The Brownian motion can be modeled by a random walk. Random walks in porous media or fractals are anomalous. In the general case, Brownian motion is a non-Markov random process and described by stochastic integral equations.
References
https://en.wikipedia.org/wiki/Stochastic_process
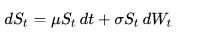
Comments