11_R
- hrafnulf13
- Nov 2, 2020
- 1 min read
Updated: Nov 4, 2020
Arithmetic mean is the sum of all of the numbers divided by the amount of numbers [1, 2].
Similarly, the mean of a sample x1,x2,…,xn, is the sum of the sampled values divided by the number of items in the sample and usually denoted as

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:
(4 + 36 + 45 + 50 + 75) / 5 = 210/5 = 42
Geometric mean is an average that is useful for sets of positive numbers, that are interpreted according to their product (as is the case with rates of growth) and not their sum (as is the case with the arithmetic mean) [1, 2]:

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:
(4 * 36 * 45 * 50 * 75)^(1/5) = (24 300 000)^(1/5) = 30
Harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, as in the case of speed (i.e., distance per unit of time) [1, 2]:

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is:
5 / (1/4 + 1/36 + 1/45 + 1/50 + 1/75) = 5/(1/3) = 15
Relationship between AM, GM, and HM is based on satisfying these inequalities [2, 3]:

If all the values in a data set are the same, then all the three means (AM, GM and HM) will be identical. As the variability in the data increases, the difference among these means also increases [3].
References
https://towardsdatascience.com/statistical-measures-of-central-tendency-d8d4fbb70111
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3127352/#:~:text=Mean%20is%20the%20most%20commonly,refers%20to%20the%20arithmetic%20mean.
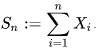
Comments