12_R
- hrafnulf13
- Nov 2, 2020
- 3 min read
Updated: Nov 4, 2020
The measure of dispersion indicates the scattering of data [1]. It explains the disparity of data from one another, delivering a precise view of the distribution of data. The measure of dispersion displays and gives us an idea about the variation and central value of an individual item. In other words, Dispersion is the extent to which values in a distribution differ from the average of the distribution. It gives us an idea about the extent to which individual items vary from one another and from the central value.
Range is the difference between the largest and the smallest observation in the data [2]. The prime advantage of this measure of dispersion is that it is easy to calculate. On the other hand, it has lot of disadvantages. It is very sensitive to outliers and does not use all the observations in a data set. It is more informative to provide the minimum and the maximum values rather than providing the range.
Range = Xmax – Xmin
It is the simplest of the measure of dispersion
Easy to calculate
Easy to understand
Independent of change of origin
It is based on two extreme observations. Hence, get affected by fluctuations
A range is not a reliable measure of dispersion
Dependent on change of scale
Interquartile Range is defined as the difference between the 25th and 75th percentile (also called the first and third quartile) [2]. Hence the interquartile range describes the middle 50% of observations. If the interquartile range is large it means that the middle 50% of observations are spaced wide apart. The important advantage of interquartile range is that it can be used as a measure of variability if the extreme values are not being recorded exactly (as in case of open-ended class intervals in the frequency distribution). Other advantageous feature is that it is not affected by extreme values. The main disadvantage in using interquartile range as a measure of dispersion is that it is not amenable to mathematical manipulation.
The IQR is a measure of variability, based on dividing a data set into quartiles [4]. Quartiles divide a rank-ordered data set into four equal parts. The values that separate parts are called the first, second, and third quartiles; and they are denoted by Q1, Q2, and Q3, respectively.
IQR = Q3 − Q1
All the drawbacks of Range are overcome by quartile deviation
It uses half of the data
Independent of change of origin
The best measure of dispersion for open-end classification
It ignores 50% of the data
Dependent on change of scale
Not a reliable measure of dispersion
Standard Deviation is the most commonly used measure of dispersion. It is a measure of spread of data about the mean [2, 5]. SD is the square root of sum of squared deviation from the mean divided by the number of observations. In a very basic sense, the standard deviation gives the sense of how the actual values of the data set vary from the mean. A high standard deviation means that the data set vary a lot, but a low standard deviation means that the data do not vary very much. the smaller the standard deviation, the better.
The standard deviation of a sample is calculated by

Squaring the deviations overcomes the drawback of ignoring signs in mean deviations
Suitable for further mathematical treatment
Least affected by the fluctuation of the observations
The standard deviation is zero if all the observations are constant
Independent of change of origin
Not easy to calculate
Difficult to understand for a layman
Dependent on the change of scale
Variance is similar to standard deviation [5]. In fact, it can be easily calculated one from another. Essentially, variance is a more precise measure of how precise the data is. It is represented by s2 for a sample and σ2 for a population. The variance is calculated as the square of the standard deviation, for both the sample and the population
The formal formula is

References
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3198538/
https://magoosh.com/statistics/measures-of-dispersion-explained/
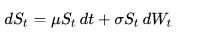
Comments