19_R
- hrafnulf13
- Dec 2, 2020
- 1 min read
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value [1].Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.
Important special cases of the order statistics are the minimum and maximum value of a sample, and (with some qualifications discussed below) the sample median and other sample quantiles.
When using probability theory to analyze order statistics of random samples from a continuous distribution, the cumulative distribution function is used to reduce the analysis to the case of order statistics of the uniform distribution.
Full demonstration can be seen here: https://demonstrations.wolfram.com/DistributionsOfOrderStatistics/
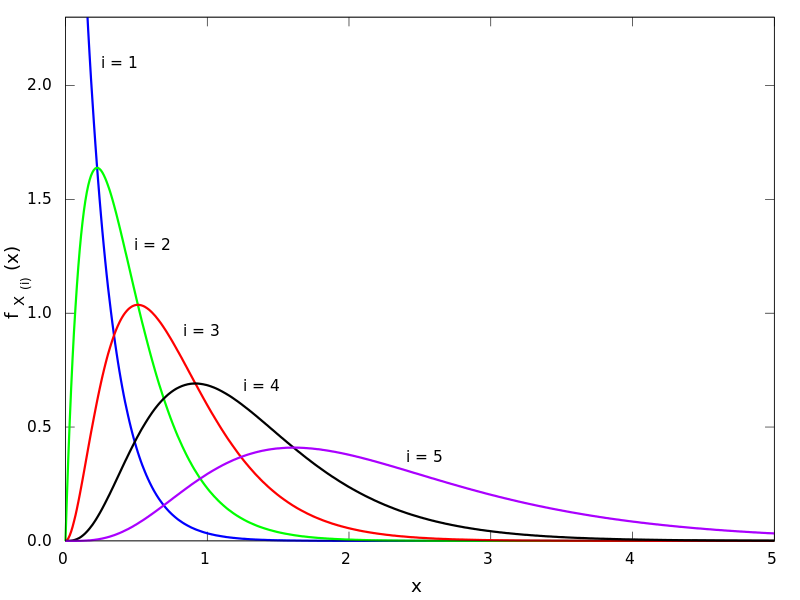
Derivations of distributions can be seen in [3].
Also nice examples can be viewed in [4].
References
https://demonstrations.wolfram.com/DistributionsOfOrderStatistics/
https://en.wikipedia.org/wiki/Order_statistic#Probability_distributions_of_order_statistics
https://online.stat.psu.edu/stat415/book/export/html/834
Comments